| Chuyên ngành đào tạo: | PHƯƠNG PHÁP TOÁN SƠ CẤP (Elementary Mathematics Methods) |
| Mã chuyên ngành: | 846 01 13 |
| Ngành: | Toán học |
| Bậc đào tạo: | Thạc sĩ |
| Thời gian đào tạo: | 2 năm |
| Tên văn bằng: | Thạc sĩ Phương pháp Toán sơ cấp |
| Đơn vị đào tạo: | Trường Đại học Khoa học - Đại học Thái Nguyên |
MỤC TIÊU ĐÀO TẠO
- Làm chủ được các kiến thức chuyên ngành về phương pháp toán sơ cấp; có khả năng giải quyết những vấn đề thực tiễn nảy sinh từ giảng dạy toán sơ cấp sử dụng các kiến thức toán cao cấp học được; có tư duy phản biện, và có khả năng tự học, nghiên cứu chuyên sâu để lĩnh hội kiến thức mới và nghiên cứu ở trình độ Tiến sĩ cùng chuyên ngành hoặc chuyên ngành Phương pháp giảng dạy Toán; có kiến thức tổng hợp về pháp luật, xã hội;
- Có kỹ năng hoàn thành các nhiệm vụ giảng dạy phức tạp như ôn luyện học sinh giỏi, học sinh thi olympic, đòi hòi tư duy độc lập, sáng tạo; có kỹ năng thử nghiệm các giải pháp mới, không dập khuôn, máy móc khi giải quyết những vấn đề phi truyền thống sử dụng những kiến thức, phương pháp được học;
- Có kỹ năng quan sát tìm tòi, phát hiện và giải quyết vấn đề trong giảng dạy toán sơ cấp một cách độc lập; có khả năng tự phát triển năng lực cá nhân và thích nghi cao với môi trường làm việc; đưa ra được những kết luận dựa trên những nguyên lý toán học, tự tin bảo vệ quan điểm và chịu trách nhiệm về những kết luận đó; có khả năng độc lập xây dựng, thẩm định các kế hoạch, dự án; quản lý dự án, phát huy trí tuệ, sức mạnh của tập thể để hoàn thành dự án cũng như các công việc được giao.
VỊ TRÍ LÀM VIỆC SAU KHI TỐT NGHIỆP
- Giảng dạy các học phần/mảng kiến thức liên quan đến toán sơ cấp trong các trường đại học, cao đẳng, trung học sư phạm hoặc giảng dạy toán ở các trường phổ thông.
- Công tác tại các viện nghiên cứu giáo dục, các sở, phòng giáo dục.
- Có thể học tiếp ở trình độ tiến sĩ.
Tìm hiểu cựu sinh viên khoa Toán - Tin: Tại đây
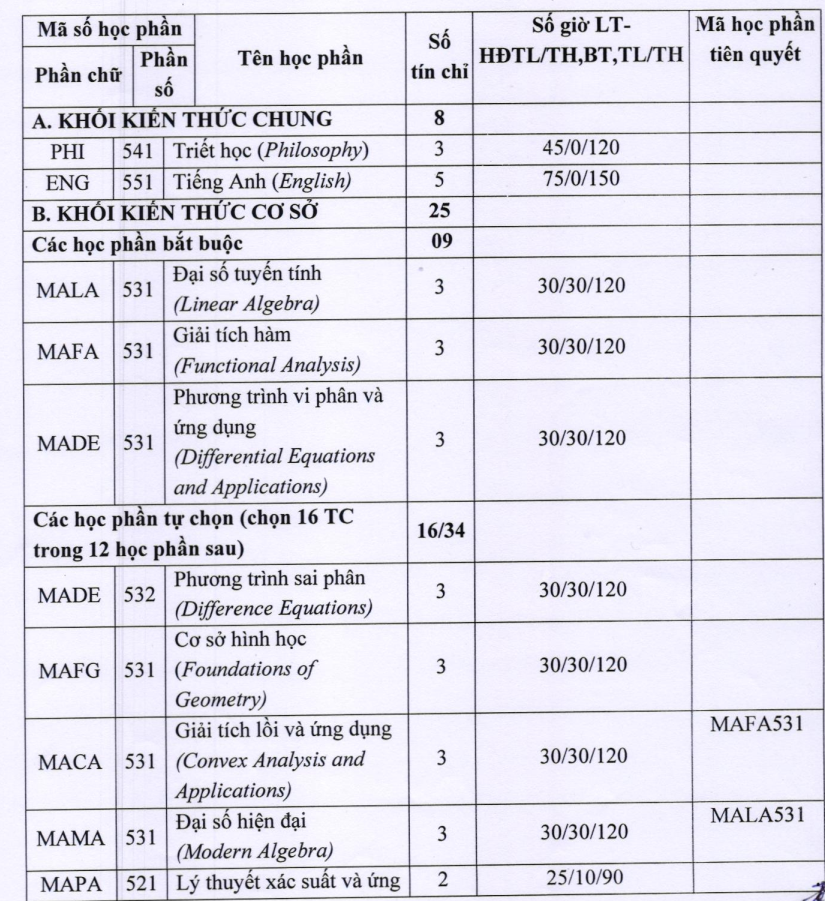
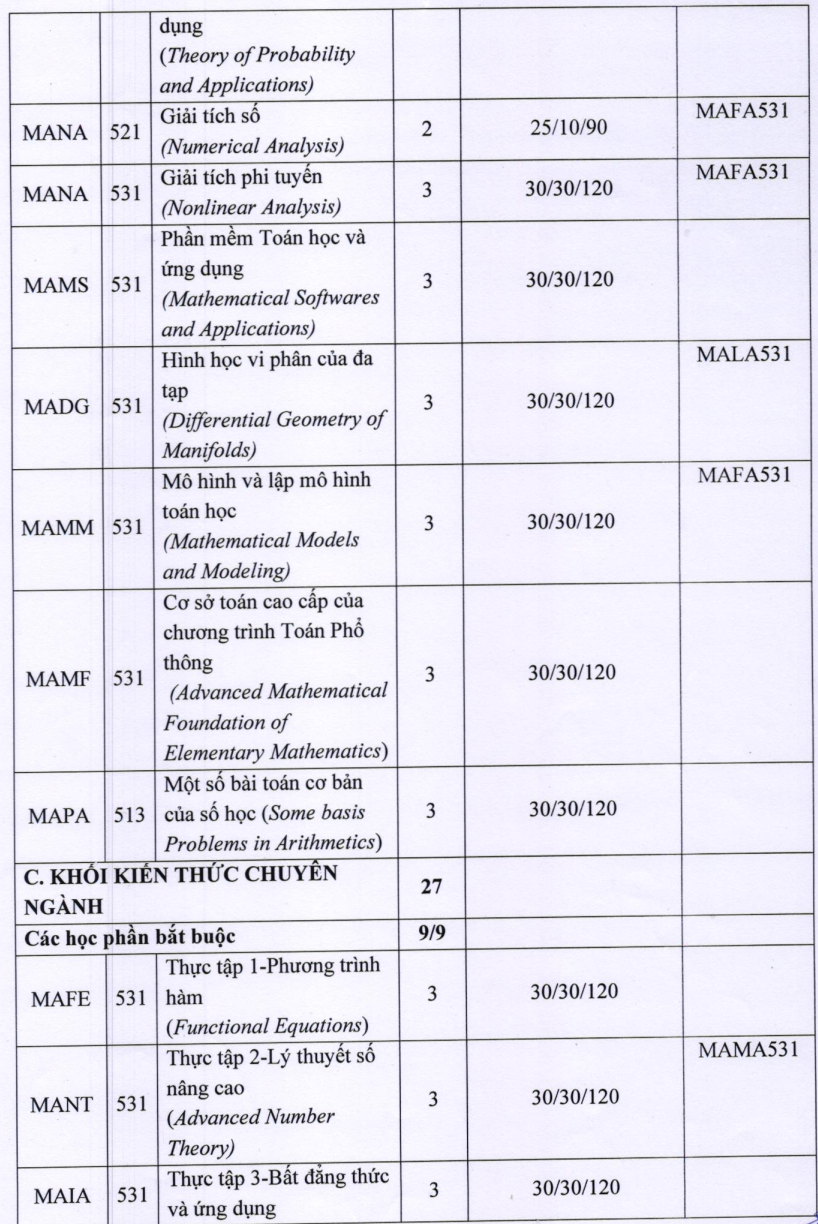
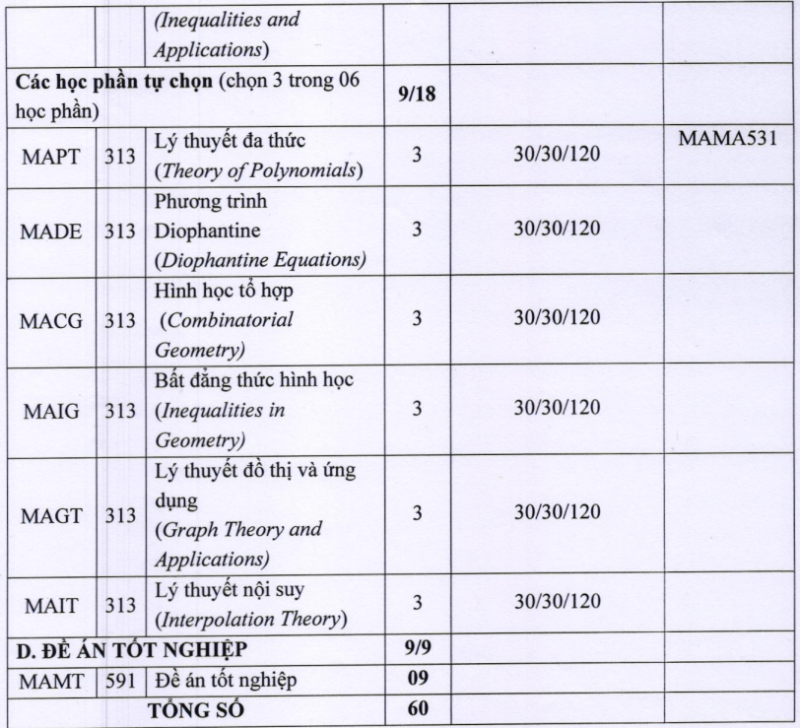
CHƯƠNG TRÌNH ĐÀO TẠO
Danh mục các học phần bắt buộc
| Kiến thức chung |
|||
| 1 | Triết học | 2 | Tiếng Anh |
| Kiến thức cơ sở |
|||
| 1 | Cơ sở giải tích lồi | 2 | Đại số tuyến tính ứng dụng |
| 3 | Đại số hiện đại | 4 | Giải tích hàm |
| 5 | Lý thuyết xác suất và ứng dụng | 6 | Giải tích số |
| 7 | Phần mềm toán học và ứng dụng | 8 | Tô pô |
| 9 | Phương trình vi phân và ứng dụng | 10 | Cơ sở hình học |
| 11 | Hình học vi phân | 12 | Thuật toán và độ phức tạp tính toán |
| Kiến thức chuyên ngành | |||
| 1 | Phương trình hàm | 2 | Lý thuyết đa thức |
| 3 | Lý thuyết số | 4 | Bất đẳng thức và ứng dụng |
| 5 | Phương trình Diophant | 6 | Hình học tổ hợp |
| 7 | Bất đẳng thức hình học | 8 | Ứng dụng của giải tích lồi vào những bài toán sơ cấp |
| 9 | Phương pháp vectơ | 10 | Một số chủ đề chọn lọc về hình học |
| Luận văn thạc sĩ | |||
Nội dung một số học phần bắt buộc
Cơ sở giải tích lồi
Cung cấp những kiến thức cơ bản về các công cụ giải tích trên hai đối tượng toán học là tập hợp lồi và hàm lồi, làm cơ sở cho các môn học chuyên ngành.
Đại số hiện đại
Học phần phát triển kế thừa và nâng cao những kiến thức đã học trong chương trình Đại số trừu tượng ở bậc đại học. Bằng việc nghiên cứu các nhóm, vành, đa thức và trường, học viên có thể hiểu được bản chất các cấu trúc đại số và có một nền tảng vững chắc để tiếp cận những vấn đề chuyên sâu hơn. Học phần còn bao gồm các nội dung mới: Lý thuyết môđun, phạm trù - hàm tử và nhập môn Đại số đồng điều.
Đại số tuyến tính ứng dụng
Học phần phát triển kế thừa và nâng cao những kiến thức đã học trong chương trình Đại số tuyến tính ở bậc đại học. Học viên được ôn lại một cách ngắn gọn các khái niệm vectơ, ma trận, định thức hệ phương trình tuyến tính, véc tơ riêng và giá trị riêng. Sau đó, học viên sẽ được cung cấp những kiến thức mang tính ứng dụng của đại số tuyến tính như phân tích giá trị kỳ dị của ma trận, bài toán giá trị riêng với chú trọng đến thuật toán tính toán, lập trình trên máy tính để giải những bài toán cỡ lớn.
Giải tích hàm
Học phần phát triển kế thừa và nâng cao những kiến thức đã học trong chương trình Giải tích hàm ở bậc đại học. Học viên được làm quen với những khái niệm cơ bản, các nguyên lý, các phương pháp của giải tích hàm cũng như các ứng dụng của nó. Học phần bao gồm các nội dung: không gian véc tơ định chuẩn, không gian Banach, toán tử tuyến tính, phiếm hàm tuyến tính và tính liên tục, các nguyên lý cơ bản của giải tích hàm, không gian liên hợp, tôpô yếu, không gian Hilbert, toán tử compact. Trên cơ sở đó, học phần cung cấp cho học viên một số nội dung cơ bản về cấu trúc hình học của các không gian Banach như tính lồi và tính trơn như không gian lồi chặt, không gian lồi đều, không gian trơn, không gian trơn đều cùng với các đặc trưng của chúng.
Lý thuyết xác suất và ứng dụng
Học phần phát triển kế thừa và nâng cao những kiến thức đã học trong chương trình Lý thuyết xác suất ở bậc đại học. Học viên được cung cấp các kiến thức về xác suất và phân phối xác suất, quá trình ngẫu nhiên, tích phân ngẫu nhiên và phương trình ngẫu nhiên, các bài toán xác suất ứng dụng.
Giải tích số
Chuyên đề giới thiệu các kiến thức cơ bản và nâng cao về các phương pháp giải gần đúng phương trình phi tuyến, phương pháp số trong đại số tuyến tính bài toán giá trị ban đầu và bài toán biên của phương trình vi phân thường và phương trình vi phân, phương trình đạo hàm riêng và phương trình tích phân.
Cơ sở hình học
Môn học này nhằm mục đích trang bị cho học viên những kiến thức nền tảng và hết sức cơ bản về việc xây dựng lý thuyết hình học bằng phương pháp tiên đề. Trong đó có hình học Euclide, hình học afin Euclide, hình học phi Euclide (Lobachevsky và Riemann nghĩa hẹp), và một số hệ tiên đề khác nhau của các hình học đó (hệ tiên đề Euclide-Hilbert, hệ tiên đề Weyl và hệ tiên đề Pogorelov…).
Phần mềm toán học và ứng dụng
Học phần cung cấp cho học viên kiến thức về chức năng của một vài phần mềm Toán học phổ biến hiện nay. Nó giúp học viên sử dụng phần mềm toán học trong tính toán (số học, giải tích, đại số tuyến tính, hình học) và minh họa kết quả, ý nghĩa trực quan của lời giải bài toán cũng như hỗ trợ việc mô hình hóa toán học.
Thuật toán và độ phức tạp tính toán
Học phần giới thiệu cho học viên nền tảng cơ sở về lý thuyết độ phức tạp và một số vấn đề liên quan. Học viên được học các thành tựu lý thuyết và thực hành về thuật toán, các kĩ thuật của thuật toán, phân tích hiệu quả và chất lượng của thuật toán, cấu trúc dữ liệu, thuật toán lý thuyết đồ thị, thuật toán xấp xỉ số và thuật toán ma trận.
Phương trình hàm
Trình bày cơ sở và lý thuyết các phương trình hàm cơ bản. Đặc biệt, tập trung vào lớp các phương trình hàm với cặp biến tự do trong lớp hàm liên tục. Xét các phương trình hàm sinh bởi các phép biến hình, các dịch chuyển đối số, các hàm số tuần hoàn cộng tính và nhân tính.
Lý thuyết số
Học phần bao gồm những chuyên đề sơ cấp về lý thuyết số và ứng dụng. Học viên được giới thiệu chi tiết một số vấn đề cơ bản trong lý thuyết số và tóm lược những thành quả sâu sắc như số nguyên tố Mersenne, sàng nguyên tố, mã RSA, đường cong eliptic...
Phương trình Diophant
Trình bày cơ sở lý thuyết của các phương trình Diophant và phương pháp xấp xỉ Diophant trong tập các số nguyên và các số tự nhiên. Tiếp theo, áp dụng khảo sát các bài toán liên quan về liên phân số, về đồng dư,…
Lý thuyết đa thức
Học phần cung cấp cho học viên những kiến thức cơ bản về vành đa thức, vành các chuỗi luỹ thừa và một số áp dụng trong toán sơ cấp. Học viên được học các chủ đề về nghiệm và xấp xỉ nghiệm của đa thức, đa thức bất khả quy và tính chia hết, ước chung lớn nhất của các đa thức, chuỗi luỹ thừa, dãy Fibonacci, dãy Catalan, dãy Stirling, đa thức Chebyshev, đa thức Bernoulli, hàm Zeta-Riemann, các số vô tỉ e và pi.
Bất đẳng thức và ứng dụng
Trình bày cơ sở lý thuyết các bất đẳng thức cơ bản, đặc biệt đi sâu khảo sát các bất đẳng thức liên quan đến quy hoạch, ước lượng và nội suy không gian, trình bày các ứng dụng trong các bài toán cực trị, trong giải và biện luận phương trình và bất phương trình, trong hình học và số học,…
Hình học tổ hợp
Môn học nhằm trang bị cho học viên những kiến thức cơ bản và nâng cao về hình học tổ hợp và một số ứng dụng trong toán học phổ thông.
Bất đẳng thức hình học
Học phần cung cấp cho học viên lý thuyết bất đẳng thức liên quan đến các độ đo (góc, độ dài, diện tích, ...) trong hình học. Các nội dung bao gồm: Bất đẳng thức Pythagore, bất đẳng thức tam giác, bất đẳng thức trong đa giác và trong đường tròn, bất đẳng thức lượng giác và một số phương pháp giải các bất đẳng thức này.
Lý thuyết đồ thị và ứng dụng
Môn học nhằm trang bị cho học viên những kiến thức cơ bản và nâng cao về lý thuyết đồ thị và khả năng ứng dụng phong phú của lý thuyết đồ thị. Đồng thời cũng giúp học viên nắm được khả năng biểu diễn đa dạng của đồ thị. Trên cơ sở đó biết chuyển các bài toán “không mẫu mực” về dạng đồ thị, rồi vận dụng các kết quả của lý thuyế đồ thị để giải quyết.
Ứng dụng của giải tích lồi vào những bài toán sơ cấp
Những kiến thức cơ bản của giải tích lồi được nhắc lại. Sau đó, thời lượng chính của học phần được dành cho các ứng dụng giải tích lồi vào các bài toán hình học, các bài toán đại số, các bài toán biện luận phương trình và bất phương trình.
Phương pháp véctơ
Trình bày cơ sở lý thuyết và ứng dụng của phương pháp véctơ giải các bài toán hình học, lượng giác và đại số. Đặc biệt khảo sát sâu phương pháp véctơ gắn với phương pháp tọa độ.
Tìm hiểu thêm tại Website: Khoa Toán - Tin
